ԴՈՒԲՆԱՅՈՒՄ ԱԱԳԼ-Ն ԵՎ ՄՀՄԻ-Ն ՍՏՈՐԱԳՐԵՑԻՆ ՀԱՄԱԳՈՐԾԱԿՑՈՒԹՅԱՆ ՀԱՄԱՁԱՅՆԱԳԻՐ
Հրապարակված է՝ 01/04/2024
Սեմինար նվիրված Նորայր Ակոպովի 75 ամյակին
Հրապարակված է՝ 19/01/2024
VI Մատինյանին նվիրված սեմինար
Հրապարակված է՝ 04/01/2024
LARES-2 արբանյակի առաջին արդյունքների հրապարակումը
Հրապարակված է՝ 22/12/2023
«Մասնիկների ֆիզիկա և կոսմոլոգիա » միջազգային գիտաժողով նվիրված պրոֆ.Ռուբակովի հիշատակին
Հրապարակված է՝ 11/10/2023
ԿԱՅԱՑԱՎ ԲԱՐՁՐ ԷՆԵՐԳԻԱՅԻ ՏԵՍԱԿԱՆ ԵՎ ՓՈՐՁԱՐԱՐԱԿԱՆ ՖԻԶԻԿԱՅԻՆ ՆՎԻՐՎԱԾ CHEP-2023-YEREVAN ԳԻՏԱԺՈՂՈՎԸ
Հրապարակված է՝ 30/09/2023
Մաթեմատիկական ֆիզիկայի արդի խնդիրներին նվիրված աշխատաժողով և ամառային դպրոց
Հրապարակված է՝ 18/08/2023
2021-2023 թթ. շրջանավարտների դիպլոմների հանձնման արարողությունը
Հրապարակված է՝ 18/07/2023
ՀԱՅ ԲԺԻՇԿՆԵՐԻ ՄԻՋԱԶԳԱՅԻՆ ԿՈՄԻՏԵԻ (AMIC) ՆԵՐԿԱՅԱՑՈՒՑԻՉՆԵՐԻ ԱՅՑՆ ԱԱԳԼ
Հրապարակված է՝ 18/07/2023
ԼԵՎ ԼԱՆԴԱՈՒԻ 115-ԱՄՅԱԿԻՆ ՆՎԻՐՎԱԾ ԳԻՏԱԺՈՂՈՎ
Հրապարակված է՝ 16/06/2023
ՀՈԲԵԼՅԱՆԱԿԱՆ ՈՒՂԵՐՁ ՀԱՐԳԱՐԺԱՆ ՊԱՐՈՆ Հ. ԳՈՒԼՔԱՆՅԱՆԻՆ
Հրապարակված է՝ 12/06/2023
Գիտաժողով նվիրված Հրանտ Գուլքանյանի 80 ամյակին
Հրապարակված է՝ 08/06/2023
«ՆՈՐ ՍԱՐՔԵՐ ՖԻԶԻԿԱՅԻ ԱՇԽԱՐՀԸ ԲԱՑԱՀԱՅՏԵԼՈՒ ՀԱՄԱՐ»․ Առաջին ալիք
Հրապարակված է՝ 25/05/2023
ԱԱԳԼ-ՈՒՄ ԿԱՅԱՑԱՎ ԶԻԳԵՆԻ ՀԱՄԱԼՍԱՐԱՆԻ ՊՐՈՖԵՍՈՐ ԱԼԵՔՍԱՆԴՐ ԽՈՋԱՄԻՐՅԱՆԻ ՍԵՄԻՆԱՐԸ
Հրապարակված է՝ 22/05/2023 (1).png)
2023-2024 ԹԹ. ՈՒՍՈՒՄՆԱԿԱՆ ՏԱՐՎԱ ԱԱԳԼ ԱՌԿԱ ՈՒՍՈՒՑՄԱՄԲ ՄԱԳԻՍՏՐԱՏՈՒՐԱՅԻ ԸՆԴՈՒՆԵԼՈՒԹՅԱՆ ՀԱՅՏԱՐԱՐՈՒԹՅՈՒՆ
Հրապարակված է՝ 22/05/2023
ԱՌԱՋԻՆ ԱԼԻՔ-Ն ԱՆԴՐԱԴԱՐՁԵԼ Է ԱԱԳԼ ՏՆՕՐԵՆ ԳԵՎՈՐԳ ՔԱՌՅԱՆԻ ԾՐԱԳՐԵՐԻՆ ՈՒ ՆՊԱՏԱԿՆԵՐԻՆ
Հրապարակված է՝ 18/05/2023
ԱԱԳԼ-Ն ՄԱՍՆԱԿՑԵՑ «ԲանՈւԳործ ԵՊՀ էքսպո-2023» ՑՈՒՑԱՀԱՆԴԵՍԻՆ
Հրապարակված է՝ 18/05/2023
ՊՐՈՖԵՍՈՐ ՄՈՍԿՈՎ ԱՄԱՐՅԱՆԻ ՍԵՄԻՆԱՐՆ ԱԱԳԼ-ՈՒՄ
Հրապարակված է՝ 17/05/2023

«ԱՅՍ ՏԱՐԻ ՏԻԵԶԵՐՔ ԿԱՐՁԱԿՎԻ ՀԱՅԿԱԿԱՆ ԱՐՏԱԴՐՈՒԹՅԱՆ ԱՐԲԱՆՅԱԿ». ԼՈՒՐԵՐ
Հրապարակված է՝ 15/05/2023
ԳԵՐՄԱՆԻԱՅԻ ԶԻԳԵՆԻ ՀԱՄԱԼՍԱՐԱՆԻ ՊՐՈՖԵՍՈՐ ԱԼԵՔՍԱՆԴՐ ԽՈՋԱՄԻՐՅԱՆԸ ԴԱՍԱԽՈՍՈՒԹՅՈՒՆՆԵՐ ԿՎԱՐԻ ԱԱԳԼ-ՈՒՄ
Հրապարակված է՝ 12/05/2023
ԱԼԻԽԱՆՅԱՆԻ ԱՆՎԱՆ ԱԶԳԱՅԻՆ ԳԻՏԱԿԱՆ ԼԱԲՈՐԱՏՈՐԻԱՆ ԿՄԱՍՆԱԿՑԻ «ԲանՈՒԳործ․ ԵՊՀ ԷՔՍՊՈ-2023»-ԻՆ
Հրապարակված է՝ 08/05/2023.jpg)
ԱԱԳԼ-ՈՒՄ ԿԱՅԱՑԱՎ «ՌԱԴԻՈ-ՀԱՃԱԽՈՒԹՅՈՒՆՆԵՐԻ ԺԱՄԱՆԱԿԱՉԱՓ» ՀԱՄԱԳՈՐԾԱԿՑՈՒԹՅԱՆ ԳԻՏԱԺՈՂՈՎԸ
Հրապարակված է՝ 08/05/2023
«ԲԱԶՈՒՄՔԻ» ՃԱՐՏԱՐԱԳԵՏՆԵՐԸ ԳԻՏԱՏԵԽՆԻԿԱԿԱՆ ԱՇԽԱՏԱՆՔՆԵՐ ԵՆ ԻՐԱԿԱՆԱՑՆՈՒՄ «ՄԱՔՈՒՐ ՍԵՆՅԱԿՈՒՄ»
Հրապարակված է՝ 08/05/2023
ԳԵՎՈՐԳ ՔԱՌՅԱՆՆ ԱԼԻԽԱՆՅԱՆԻ ԱՆՎԱՆ ԱԶԳԱՅԻՆ ԳԻՏԱԿԱՆ ԼԱԲՈՐԱՏՈՐԻԱՅԻ ՆՈՐ ՏՆՕՐԵՆՆ Է
Հրապարակված է՝ 05/05/2023
ՀԱՄԱԳՈՐԾԱԿՑՈՒԹՅԱՆ ՀԱՄԱԺՈՂՈՎ՝ ԱԱԳԼ-ՈՒՄ
Հրապարակված է՝ 02/05/2023
ԱԱԳԼ ԳԻՏՆԱԿԱՆՆԵՐՆ ԱՊՐԻԼԻ 18-ԻՆ SEVAN ԴԵՏԵԿՏՈՐԸ ՏԵՂԱԴՐԵՑԻՆ ԲԱՎԱՐԱԿԱՆ ԱԼՊԵՐԻ ՑՈՒԳՇՊԻՑԵ ԼԵՌԱՆ ՎՐԱ
Հրապարակված է՝ 28/04/2023.jpg)
«ՄԵՆՔ ԿԱՐՈՂ ԵՆՔ ՓՈԽԵԼ ԱՇԽԱՐՀԸ ԳԻՏՈՒԹՅԱՄԲ, ԲԱՅՑ ՆԱԽ ՊԵՏՔ Է ՍԿՍԵԼ ՀԱՅԱՍՏԱՆԻՑ»․ ԱՆԻ ԱՊՐԱՀԱՄՅԱՆ
Հրապարակված է՝ 27/04/2023
ԹԵԿՆԱԾՈՒԱԿԱՆ ԱՏԵՆԱԽՈՍՈՒԹՅԱՆ ՊԱՇՏՊԱՆՈՒԹՅՈՒՆ
Հրապարակված է՝ 26/04/2023.jpg)
ՄՐՑՈՒՅԹ
Հրապարակված է՝ 26/04/2023
ՄԵՐ ԳՈՐԾԵՐԸ ՄՐՑՈՒՆԱԿ ԵՆ ԱՄԲՈՂՋ ԱՇԽԱՐՀՈՒՄ. ԱՎԵԼԻՆ ԿԱՐՈՂ ԷԻՆՔ ԱՆԵԼ
Հրապարակված է՝ 21/04/2023
ԱԱԳԼ ՏՆՕՐԵՆԸ՝ «ՆՈՐԱՐԱՐՈՒԹՅԱՆ ԵՎ ՁԵՌՆԵՐԵՑՈՒԹՅԱՆ ԱԶԳԱՅԻՆ ՇԱԲԱԹԻ» ՔՆՆԱՐԿՄԱՆ ՎԱՐՈՂ
Հրապարակված է՝ 20/04/2023
«ՄԵՆՔ ՊԵՏՔ Է ՆՈՐ ՈՒԺ ՏԱՆՔ ՀԱՅԱՍՏԱՆՈՒՄ ՄԻՋՈՒԿԱՅԻՆ ՖԻԶԻԿԱՅԻ ԶԱՐԳԱՑՄԱՆԸ». ԱՆԻ ԱՊՐԱՀԱՄՅԱՆ
Հրապարակված է՝ 18/04/2023
ՅՈՒՐԻ ՀՈՎՀԱՆՆԻՍՅԱՆԻ 90-ՐԴ ՏԱՐԵԴԱՐՁԸ
Հրապարակված է՝ 18/04/2023
Առաջին ալիքի անդրադարձը՝ քվանտային տեղեկատվական և քվանտային տեխնոլոգիաների բաժանմունքին
Հրապարակված է՝ 10/03/2023ՄՐՑՈՒՅԹ՝ ԱԱԳԼ ԿԱՌԱՎԱՐԻՉ-ՏՆՕՐԵՆԻ ԹԱՓՈՒՐ ՊԱՇՏՈՆԻ ՀԱՄԱԼՐՄԱՆ ՀԱՄԱՐ
Հրապարակված է՝ 10/03/2023.jpg)
ԱՇԽԱՏԱԺՈՂՈՎ՝ ՆՎԻՐՎԱԾ ՌՈՒԲԵՆ ՄԱՆՎԵԼՅԱՆԻ 60-ԱՄՅԱԿԻՆ
Հրապարակված է՝ 09/03/2023
STARMUS VI ՓԱՌԱՏՈՆԻ ԳԻՏԱԿԱՆ ԵՎ ՄՇԱԿՈՒԹԱՅԻՆ ԱՆՄՈՌԱՆԱԼԻ ՕՐԵՐՆ ԱՄՓՈՓՎԵԼ ԵՆ ՏԵՍԱՀՈԼՈՎԱԿՈՒՄ
Հրապարակված է՝ 07/03/2023
ԱԱԳԼ-Ն ԱՄՓՈՓՈՒՄ Է ԳԻՏԱԿԱՆ ՏԱՐԻՆ
Հրապարակված է՝ 07/03/2023
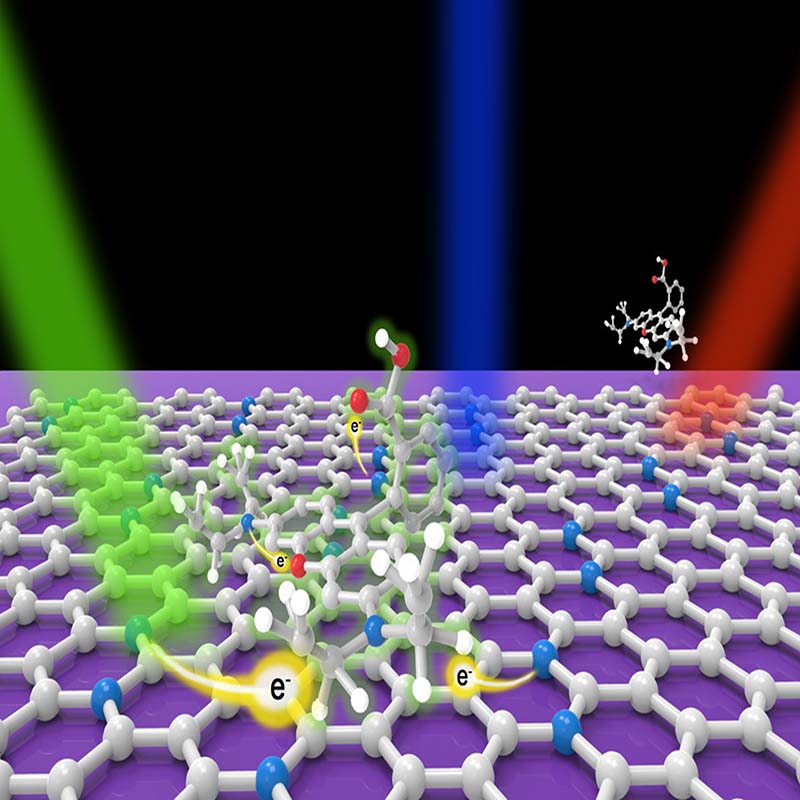
ԳՐԱՖԵՆԻ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
Հրապարակված է՝ 06/03/2023
ՓԵՏՐՎԱՐԻ 11-Ը ԳԻՏՈՒԹՅԱՆ ՄԵՋ ԿԱՆԱՆՑ ԵՎ ԱՂՋԻԿՆԵՐԻ ՄԻՋԱԶԳԱՅԻՆ ՕՐՆ Է
Հրապարակված է՝ 06/03/2023
ԱԱԳԼ փորձարարական բաժանմունքի գիտնականները՝ միջազգային նախագծերում
Հրապարակված է՝ 03/03/2023
ՈՉՀԵՐՄԻԹՅԱՆ ՖՈՏՈՆԻԿԱՅԻ ՎԵՐԱԲԵՐՅԱԼ ՍԵՄԻՆԱՐ՝ ԱԱԳԼ-ՈՒՄ
Հրապարակված է՝ 03/03/2023
V Մատինյանի հիշատակին նվիրված սեմինար
Հրապարակված է՝ 22/01/2023
IV Մատինյանի հիշատակին նվիրված սեմինար
Հրապարակված է՝ 22/01/2022
III Մատինյանի հիշատակին նվիրված սեմինար
Հրապարակված է՝ 22/01/2021
II Մատինյանի հիշատակին նվիրված սեմինար
Հրապարակված է՝ 22/01/2020
I Մատինյանի հիշատակին նվիրված սեմինար
Հրապարակված է՝ 22/01/2019Հունվար 08
Հուլիս 13
Հունվար 09
Հունվար 08
Հունվար 08
Հունվար 08
Հունվար 18

«ՆՈՐ ՍԱՐՔԵՐ ՖԻԶԻԿԱՅԻ ԱՇԽԱՐՀԸ ԲԱՑԱՀԱՅՏԵԼՈՒ ՀԱՄԱՐ»․ Առաջին ալիք
Հրապարակված է՝ 25/05/2023
ԱՌԱՋԻՆ ԱԼԻՔ-Ն ԱՆԴՐԱԴԱՐՁԵԼ Է ԱԱԳԼ ՏՆՕՐԵՆ ԳԵՎՈՐԳ ՔԱՌՅԱՆԻ ԾՐԱԳՐԵՐԻՆ ՈՒ ՆՊԱՏԱԿՆԵՐԻՆ
Հրապարակված է՝ 18/05/2023
«ԱՅՍ ՏԱՐԻ ՏԻԵԶԵՐՔ ԿԱՐՁԱԿՎԻ ՀԱՅԿԱԿԱՆ ԱՐՏԱԴՐՈՒԹՅԱՆ ԱՐԲԱՆՅԱԿ». ԼՈՒՐԵՐ
Հրապարակված է՝ 15/05/2023
«ՀԱՅԱՍՏԱՆՈՒՄ ԲԱՑՎԵԼ Է ԱՌԱՋԻՆ ՄԱՔՈՒՐ ՍԵՆՅԱԿԸ». ԻՆՖՈՔՈՄ ԼՐԱՏՎԱԿԱՆ
Հրապարակված է՝ 10/05/2023
ԻՆՉՊԵ՞Ս Է ԶԱՐԳԱՆՈՒՄ ՖՈՒՆԴԱՄԵՆՏԱԼ ԳԻՏՈՒԹՅՈՒՆԸ ՀԱՅԱՍՏԱՆՈՒՄ. ՀԱՆՐԱՅԻՆ ՌԱԴԻՈՅԻ ԱՆԴՐԱԴԱՐՁԸ
Հրապարակված է՝ 26/04/2023
«ԳԻՏԱՐԲՈՒՔԸ» ՀՅՈՒՐԸՆԿԱԼԵԼ ԷՐ ԳԵՎՈՐԳ ՔԱՌՅԱՆԻՆ
Հրապարակված է՝ 26/04/2023
ՄԵՐ ԳՈՐԾԵՐԸ ՄՐՑՈՒՆԱԿ ԵՆ ԱՄԲՈՂՋ ԱՇԽԱՐՀՈՒՄ. ԱՎԵԼԻՆ ԿԱՐՈՂ ԷԻՆՔ ԱՆԵԼ
Հրապարակված է՝ 21/04/2023.jpg)
ՕՐԸ ԳԻՏՆԱԿԱՆԻ ՀԵՏ. ԱՇԱԿԵՐՏՆԵՐԸ ՄԻ ՔԱՆԻ ՕՐ ԱՊՐՈՒՄ ԵՆ «ԳԻՏՆԱԿԱՆԻ ԿՅԱՆՔՈՎ»
Հրապարակված է՝ 18/04/2023
«ՄԵՆՔ ՊԵՏՔ Է ՆՈՐ ՈՒԺ ՏԱՆՔ ՀԱՅԱՍՏԱՆՈՒՄ ՄԻՋՈՒԿԱՅԻՆ ՖԻԶԻԿԱՅԻ ԶԱՐԳԱՑՄԱՆԸ». ԱՆԻ ԱՊՐԱՀԱՄՅԱՆ
Հրապարակված է՝ 18/04/2023
ՅՈՒՐԻ ՀՈՎՀԱՆՆԻՍՅԱՆԻ 90-ՐԴ ՏԱՐԵԴԱՐՁԸ
Հրապարակված է՝ 18/04/2023
1000 ԴԱՍԻ «ՄԱՔՈՒՐ ՍԵՆՅԱԿԻ» ԲԱՑՄԱՆ ԱՐԱՐՈՂՈՒԹՅՈՒՆԸ
Հրապարակված է՝ 18/04/2023
Առաջին ալիքի անդրադարձը՝ քվանտային տեղեկատվական և քվանտային տեխնոլոգիաների բաժանմունքին
Հրապարակված է՝ 10/03/2023

Պերովսկիտի առավելություններն ու թերությունները
Հրապարակված է՝ 06/03/2023
ԱԱԳԼ փորձարարական բաժանմունքի գիտնականները՝ միջազգային նախագծերում
Հրապարակված է՝ 03/03/2023